pomp
Inference for partially observed Markov processes
Loading...
Searching...
No Matches
Functions
distributions.c File Reference
#include <R.h>
#include <Rmath.h>
#include <Rdefines.h>
#include "internal.h"
Include dependency graph for distributions.c:

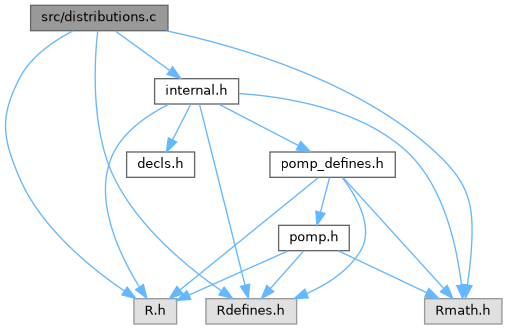
Go to the source code of this file.

Functions

static void reulermultinom_multi (int m, int n, double *size, double *rate, double *deltat, double *trans)
 
static void deulermultinom_multi (int m, int n, double *size, double *rate, double *deltat, double *trans, int *give_log, double *f)
 
SEXP R_Euler_Multinom (SEXP n, SEXP size, SEXP rate, SEXP deltat)
 
SEXP D_Euler_Multinom (SEXP x, SEXP size, SEXP rate, SEXP deltat, SEXP log)
 
SEXP E_Euler_Multinom (SEXP size, SEXP rate, SEXP deltat)
 
SEXP R_GammaWN (SEXP n, SEXP sigma, SEXP deltat)
 
SEXP R_BetaBinom (SEXP n, SEXP size, SEXP prob, SEXP theta)
 
SEXP D_BetaBinom (SEXP x, SEXP size, SEXP prob, SEXP theta, SEXP log)
 

Function Documentation

◆ D_BetaBinom()

SEXP D_BetaBinom ( SEXP x,
SEXP size,
SEXP prob,
SEXP theta,
SEXP log )

Definition at line 137 of file distributions.c.

137 {
138 int k, n, nx, ns, np, nt;
139 double *F, *X, *S, *P, *T;
140 SEXP f;
141 PROTECT(x = AS_NUMERIC(x)); nx = LENGTH(x); X = REAL(x);
142 PROTECT(size = AS_NUMERIC(size)); ns = LENGTH(size); S = REAL(size);
143 PROTECT(prob = AS_NUMERIC(prob)); np = LENGTH(prob); P = REAL(prob);
144 PROTECT(theta = AS_NUMERIC(theta)); nt = LENGTH(theta); T = REAL(theta);
145 PROTECT(log = AS_INTEGER(log));
146 n = (nx > ns) ? nx : ns;
147 n = (n > np) ? n : np;
148 n = (n > nt) ? n : nt;
149 PROTECT(f = NEW_NUMERIC(n)); F = REAL(f);
150 for (k = 0; k < n; k++) {
151 F[k] = dbetabinom(X[k%nx],S[k%ns],P[k%np],T[k%nt],INTEGER(log)[0]);
152 }
153 UNPROTECT(6);
154 return f;
155}
X
#define X
Definition gompertz.c:14
dbetabinom
static R_INLINE double dbetabinom(double x, double size, double prob, double theta, int give_log)
Definition pomp.h:321
Here is the call graph for this function:

◆ D_Euler_Multinom()

SEXP D_Euler_Multinom ( SEXP x,
SEXP size,
SEXP rate,
SEXP deltat,
SEXP log )

Definition at line 49 of file distributions.c.

49 {
50 int ntrans = length(rate);
51 int *dim, n;
52 SEXP f;
53 dim = INTEGER(GET_DIM(x));
54 if (dim[0] != ntrans)
55 err("NROW('x') should match length of 'rate'");
56 n = dim[1];
57 if (length(size)>1)
58 warn("in 'deulermultinom': only the first element of 'size' is meaningful");
59 if (length(deltat)>1)
60 warn("in 'deulermultinom': only the first element of 'dt' is meaningful");
61 PROTECT(f = NEW_NUMERIC(n));
62 PROTECT(size = AS_NUMERIC(size));
63 PROTECT(rate = AS_NUMERIC(rate));
64 PROTECT(deltat = AS_NUMERIC(deltat));
65 PROTECT(log = AS_LOGICAL(log));
66 deulermultinom_multi(ntrans,n,REAL(size),REAL(rate),REAL(deltat),REAL(x),INTEGER(log),REAL(f));
67 UNPROTECT(5);
68 return f;
69}
deulermultinom_multi
static void deulermultinom_multi(int m, int n, double *size, double *rate, double *deltat, double *trans, int *give_log, double *f)
Definition distributions.c:15
warn
#define warn(...)
Definition pomp.h:22
err
#define err(...)
Definition pomp.h:21
Here is the call graph for this function:

◆ deulermultinom_multi()

static void deulermultinom_multi ( int m,
int n,
double * size,
double * rate,
double * deltat,
double * trans,
int * give_log,
double * f )
static

Definition at line 15 of file distributions.c.

15 {
16 int k;
17 for (k = 0; k < n; k++) {
18 f[k] = deulermultinom(m,*size,rate,*deltat,trans,*give_log);
19 trans += m;
20 }
21}
deulermultinom
static R_INLINE double deulermultinom(int m, double size, const double *rate, double dt, double *trans, int give_log)
Definition pomp.h:201
Here is the call graph for this function:
Here is the caller graph for this function:

◆ E_Euler_Multinom()

SEXP E_Euler_Multinom ( SEXP size,
SEXP rate,
SEXP deltat )

Definition at line 71 of file distributions.c.

71 {
72 int ntrans = length(rate);
73 SEXP x;
74 if (length(size)>1)
75 warn("in 'eeulermultinom': only the first element of 'size' is meaningful");
76 if (length(deltat)>1)
77 warn("in 'eeulermultinom': only the first element of 'dt' is meaningful");
78 PROTECT(size = AS_NUMERIC(size));
79 PROTECT(rate = AS_NUMERIC(rate));
80 PROTECT(deltat = AS_NUMERIC(deltat));
81 PROTECT(x = duplicate(rate));
82 eeulermultinom(ntrans,*REAL(size),REAL(rate),*REAL(deltat),REAL(x));
83 UNPROTECT(4);
84 return x;
85}
eeulermultinom
static R_INLINE void eeulermultinom(int m, double size, const double *rate, double dt, double *trans)
Definition pomp.h:138
Here is the call graph for this function:

◆ R_BetaBinom()

SEXP R_BetaBinom ( SEXP n,
SEXP size,
SEXP prob,
SEXP theta )

Definition at line 119 of file distributions.c.

119 {
120 int k, nval, ns, np, nt;
121 double *X, *S, *P, *T;
122 SEXP ans;
123 PROTECT(n = AS_INTEGER(n)); nval = INTEGER(n)[0];
124 PROTECT(size = AS_NUMERIC(size)); ns = LENGTH(size); S = REAL(size);
125 PROTECT(prob = AS_NUMERIC(prob)); np = LENGTH(prob); P = REAL(prob);
126 PROTECT(theta = AS_NUMERIC(theta)); nt = LENGTH(theta); T = REAL(theta);
127 PROTECT(ans = NEW_NUMERIC(nval)); X = REAL(ans);
128 GetRNGstate();
129 for (k = 0; k < nval; k++) {
130 X[k] = rbetabinom(S[k%ns],P[k%np],T[k%nt]);
131 }
132 PutRNGstate();
133 UNPROTECT(5);
134 return ans;
135}
rbetabinom
static R_INLINE double rbetabinom(double size, double prob, double theta)
Definition pomp.h:314
Here is the call graph for this function:

◆ R_Euler_Multinom()

SEXP R_Euler_Multinom ( SEXP n,
SEXP size,
SEXP rate,
SEXP deltat )

Definition at line 23 of file distributions.c.

23 {
24 int ntrans = length(rate);
25 int dim[2];
26 SEXP x, nm;
27 if (length(size)>1)
28 warn("in 'reulermultinom': only the first element of 'size' is meaningful");
29 if (length(deltat)>1)
30 warn("in 'reulermultinom': only the first element of 'dt' is meaningful");
31 PROTECT(n = AS_INTEGER(n));
32 PROTECT(size = AS_NUMERIC(size));
33 PROTECT(rate = AS_NUMERIC(rate));
34 PROTECT(deltat = AS_NUMERIC(deltat));
35 dim[0] = ntrans;
36 dim[1] = *INTEGER(n);
37 if (dim[1] == NA_INTEGER || dim[1] < 0)
38 err("in 'reulermultinom': 'n' must be a non-negative integer.");
39 PROTECT(x = makearray(2,dim));
40 PROTECT(nm = GET_NAMES(rate));
41 setrownames(x,nm,2);
42 GetRNGstate();
43 reulermultinom_multi(dim[0],dim[1],REAL(size),REAL(rate),REAL(deltat),REAL(x));
44 PutRNGstate();
45 UNPROTECT(6);
46 return x;
47}
reulermultinom_multi
static void reulermultinom_multi(int m, int n, double *size, double *rate, double *deltat, double *trans)
Definition distributions.c:7
setrownames
static R_INLINE void setrownames(SEXP x, SEXP names, int rank)
Definition pomp_defines.h:110
makearray
static R_INLINE SEXP makearray(int rank, const int *dim)
Definition pomp_defines.h:40
Here is the call graph for this function:

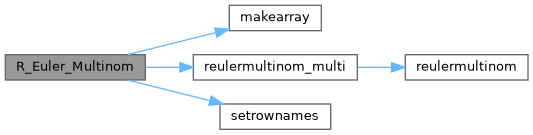
◆ R_GammaWN()

SEXP R_GammaWN ( SEXP n,
SEXP sigma,
SEXP deltat )

Definition at line 93 of file distributions.c.

93 {
94 int k, nval, nsig, ndt;
95 double *x, *sig, *dt;
96 SEXP ans;
97 PROTECT(n = AS_INTEGER(n));
98 nval = INTEGER(n)[0];
99 PROTECT(sigma = AS_NUMERIC(sigma));
100 nsig = LENGTH(sigma);
101 sig = REAL(sigma);
102 PROTECT(deltat = AS_NUMERIC(deltat));
103 ndt = LENGTH(deltat);
104 dt = REAL(deltat);
105 PROTECT(ans = NEW_NUMERIC(nval));
106 x = REAL(ans);
107 GetRNGstate();
108 for (k = 0; k < nval; k++) {
109 x[k] = rgammawn(sig[k%nsig],dt[k%ndt]);
110 }
111 PutRNGstate();
112 UNPROTECT(4);
113 return ans;
114}
sigma
#define sigma
Definition gompertz.c:93
rgammawn
static R_INLINE double rgammawn(double sigma, double dt)
Definition pomp.h:129
Here is the call graph for this function:

◆ reulermultinom_multi()

static void reulermultinom_multi ( int m,
int n,
double * size,
double * rate,
double * deltat,
double * trans )
static

Definition at line 7 of file distributions.c.

7 {
8 int k;
9 for (k = 0; k < n; k++) {
10 reulermultinom(m,*size,rate,*deltat,trans);
11 trans += m;
12 }
13}
reulermultinom
static R_INLINE void reulermultinom(int m, double size, const double *rate, double dt, double *trans)
Definition pomp.h:166
Here is the call graph for this function:
Here is the caller graph for this function: